Se le llama ecuación polar a la ecuación que define una curva expresada en coordenadas polares. En muchos casos se puede especificar tal ecuación definiendo  como una función de θ. La curva resultante consiste en una serie de puntos en la forma (
como una función de θ. La curva resultante consiste en una serie de puntos en la forma ( (θ), θ) y se puede representar como la gráfica de una función
(θ), θ) y se puede representar como la gráfica de una función  .
.
 como una función de θ. La curva resultante consiste en una serie de puntos en la forma (
como una función de θ. La curva resultante consiste en una serie de puntos en la forma ( (θ), θ) y se puede representar como la gráfica de una función
(θ), θ) y se puede representar como la gráfica de una función  .
.
Se pueden deducir diferentes formas de simetría de la ecuación de una función polar  . Si
. Si  (−θ) =
(−θ) =  (θ) la curva será simétrica respecto al eje horizontal (0°/180°), si
(θ) la curva será simétrica respecto al eje horizontal (0°/180°), si  (180°−θ) =
(180°−θ) =  (θ) será simétrica respecto al eje vertical (90°/ 270°), y si
(θ) será simétrica respecto al eje vertical (90°/ 270°), y si  (θ−α°) =
(θ−α°) =  (θ) será simétrico rotacionalmente α° en sentido horario respecto al polo.
(θ) será simétrico rotacionalmente α° en sentido horario respecto al polo.
 . Si
. Si  (−θ) =
(−θ) =  (θ) la curva será simétrica respecto al eje horizontal (0°/180°), si
(θ) la curva será simétrica respecto al eje horizontal (0°/180°), si  (180°−θ) =
(180°−θ) =  (θ) será simétrica respecto al eje vertical (90°/ 270°), y si
(θ) será simétrica respecto al eje vertical (90°/ 270°), y si  (θ−α°) =
(θ−α°) =  (θ) será simétrico rotacionalmente α° en sentido horario respecto al polo.
(θ) será simétrico rotacionalmente α° en sentido horario respecto al polo.
Debido a la naturaleza circular del sistema de coordenadas polar, muchas curvas se pueden describir con una simple ecuación polar, mientras que en su forma cartesiana sería mucho más intrincado. Algunas de las curvas más conocidas son la rosa polar, la espiral de Arquímedes, la lemniscata, el caracol de Pascal y la cardioide.
Para los apartados siguientes se entiende que el círculo, la línea y la rosa polar no tienen restricciones en el dominio y rango de la curva.
Circunferencia
Circunferencia
La ecuación general para una circunferencia con centro en ( 0, φ) y radio
0, φ) y radio  es
es
 0, φ) y radio
0, φ) y radio  es
es
En ciertos casos específicos, la ecuación anterior se puede simplificar.
Línea
Línea
donde φ es el ángulo de elevación de la línea, esto es, φ = arctan  donde
donde  es la pendiente de la línea en el sistema de coordenadas cartesianas. La línea no radial que cruza la línea radial θ = φ perpendicularmente al punto (
es la pendiente de la línea en el sistema de coordenadas cartesianas. La línea no radial que cruza la línea radial θ = φ perpendicularmente al punto ( 0, φ) tiene la ecuación
0, φ) tiene la ecuación
 donde
donde  es la pendiente de la línea en el sistema de coordenadas cartesianas. La línea no radial que cruza la línea radial θ = φ perpendicularmente al punto (
es la pendiente de la línea en el sistema de coordenadas cartesianas. La línea no radial que cruza la línea radial θ = φ perpendicularmente al punto ( 0, φ) tiene la ecuación
0, φ) tiene la ecuaciónRosa polar
La rosa polar es una famosa curva matemática que parece una flor con pétalos, y puede expresarse como una ecuación polar simple,
para cualquier constante  (incluyendo al 0). Si k es un número entero, estas ecuaciones representan una rosa de k pétalos cuando k es impar, o 2k pétalos si k es par. Si k es racional pero no entero, la gráfica es similar a una rosa pero con los pétalos solapados. Nótese que estas ecuaciones nunca definen una rosa con 2, 6, 10, 14, etc. pétalos. La variable a representa la longitud de los pétalos de la rosa.
(incluyendo al 0). Si k es un número entero, estas ecuaciones representan una rosa de k pétalos cuando k es impar, o 2k pétalos si k es par. Si k es racional pero no entero, la gráfica es similar a una rosa pero con los pétalos solapados. Nótese que estas ecuaciones nunca definen una rosa con 2, 6, 10, 14, etc. pétalos. La variable a representa la longitud de los pétalos de la rosa.
 (incluyendo al 0). Si k es un número entero, estas ecuaciones representan una rosa de k pétalos cuando k es impar, o 2k pétalos si k es par. Si k es racional pero no entero, la gráfica es similar a una rosa pero con los pétalos solapados. Nótese que estas ecuaciones nunca definen una rosa con 2, 6, 10, 14, etc. pétalos. La variable a representa la longitud de los pétalos de la rosa.
(incluyendo al 0). Si k es un número entero, estas ecuaciones representan una rosa de k pétalos cuando k es impar, o 2k pétalos si k es par. Si k es racional pero no entero, la gráfica es similar a una rosa pero con los pétalos solapados. Nótese que estas ecuaciones nunca definen una rosa con 2, 6, 10, 14, etc. pétalos. La variable a representa la longitud de los pétalos de la rosa.
Si tomamos sólo valores positivos para r y valores en el intervalo  para
para  , la gráfica de la ecuación:
, la gráfica de la ecuación:
 para
para  , la gráfica de la ecuación:
, la gráfica de la ecuación:
es una rosa de k pétalos, para cualquier número natural  . Y si
. Y si 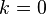 , la gráfica es una circunferencia de radio
, la gráfica es una circunferencia de radio 
 . Y si
. Y si 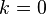 , la gráfica es una circunferencia de radio
, la gráfica es una circunferencia de radio 
Espiral de Arquímedes
La espiral de Arquímedes es una famosa espiral descubierta por Arquímedes, la cual puede expresarse también como una ecuación polar simple. Se representa con la ecuación
Un cambio en el parámetro a producirá un giro en la espiral, mientras que b controla la distancia entre los brazos, la cual es constante para una espiral dada. La espiral de Arquímedes tiene dos brazos, uno para θ > 0 y otro para θ < 0. Los dos brazos están conectados en el polo. La imagen especular de un brazo sobre el eje vertical produce el otro brazo. Esta curva fue una de las primeras curvas, después de las secciones cónicas, en ser descritas en tratados matemáticos. Además es el principal ejemplo de curva que puede representarse de forma más fácil con una ecuación polar.
Otros ejemplos de espirales son la espiral logarítmica y la espiral de Fermat.
Secciones cónicas
Una sección cónica con un foco en el polo y el otro en cualquier punto del eje horizontal (de modo que el semieje mayor de la cónica descanse sobre el eje polar) es dada por:
donde e es la excentricidad y  es el semilado recto (la distancia perpendicular a un foco desde el eje mayor a la curva). Si e > 1, esta ecuación define una hipérbola; sie = 1, define una parábola; y si e < 1, define una elipse. Para la elipse, el caso especial e = 0 resulta en un círculo de radio
es el semilado recto (la distancia perpendicular a un foco desde el eje mayor a la curva). Si e > 1, esta ecuación define una hipérbola; sie = 1, define una parábola; y si e < 1, define una elipse. Para la elipse, el caso especial e = 0 resulta en un círculo de radio  .
.
 es el semilado recto (la distancia perpendicular a un foco desde el eje mayor a la curva). Si e > 1, esta ecuación define una hipérbola; sie = 1, define una parábola; y si e < 1, define una elipse. Para la elipse, el caso especial e = 0 resulta en un círculo de radio
es el semilado recto (la distancia perpendicular a un foco desde el eje mayor a la curva). Si e > 1, esta ecuación define una hipérbola; sie = 1, define una parábola; y si e < 1, define una elipse. Para la elipse, el caso especial e = 0 resulta en un círculo de radio  .
.
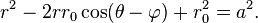
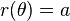






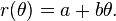

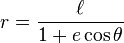
excelente teoría si colocaras un ejercicio de cónicas te agradeceria
ResponderEliminar